Pwn2Win 2019: Real EC
The CTF problem “real-ec” from Pwn2Win asked you to crack 300 low-entropy elliptic curve keys in under 100 seconds. However, the naive approach would need 1B elliptic curve operations (not going to happen), so instead I modified the famous “giant steps, baby steps” algorithm to achieve a quadratic speedup. This was still slightly too slow, so I distributed the work in real time to 5 worker nodes in a UF computer lab and finally broke the keys in under 100 seconds.
Disclaimer
This writeup may have a few incorrect or inaccurate statements about cryptography.
Problem
Pwn2Win problem from November 2019:
Our members had access to a place where a secret meeting of the Organization was happing. During the meeting, they discussed about out work in 2019 and sent detailed commands to the Squads through “Internet Relay System”. We had luck! Our group was abble to collect the service program used to authenticate the Squads, and left there without being noticed. Becuse the message self-destroys, all the Squads must be together for the reception.
Each Squad has a token (private key) that matches with a public key. The keys of all Squads must be combined and sent to the service in order to authenticate properly and get the instructions. I’m sending to you the information collected by this group. Your mission is to find out what are the next steps of the Squads and be ready for their actions. Because we are having progress, they clearly are desperate.
Server: nc 200.136.252.44 1337
Server backup: nc 167.172.225.246 1337
The server prints a list of elliptic-curve public keys corresponding to the secret. If the hash of the secret is returned to the server within 100 seconds, the server returns the key.
Target Code (annotated)
from secrets import flag
from fastecdsa import keys, curve
import hashlib
import signal
import sys
import struct
import random
import os
# on SIGALRM, halt
def handler(signum, frame):
print("\nGame over!")
sys.exit(0)
signal.signal(signal.SIGALRM, handler)
# generate secret
secret = os.urandom(1000)
# generate public keys
pub_keys = []
for i in range(0, len(secret), 4):
# read 4 bytes of secret into a big-endian int (">I")
p = struct.unpack(">I", secret[i:i+4])[0]
# create "s | s | ..{8}.. | s", where s = (p or 0^32)
n = 0
while n == 0:
for i in range(8):
n = (n << 32) + (p * random.getrandbits(1))
# generate N = nG in P-256 group
pk = keys.get_public_key(n, curve.P256)
pub_keys.append((hex(pk.x), hex(pk.y)))
# send public keys
print(pub_keys)
# halt in 100 seconds
signal.alarm(100)
# prompt for hash of secret
h = input("Tell me the hash: ")
if h == hashlib.sha256(secret).hexdigest():
print(flag)Analysis
Observations
The first thing to notice is that the elliptic curve public keys only have 40 bits of entropy – 8 from the random concatenation and 32 from the random integer. This makes them vulnerable to a brute-force attack. The problem is that elliptic curve operations are relatively slow – doing of them is not feasible in 100 seconds (maybe if you had an entire datacenter?). So, we’re gonna need to do some precomputation.
Idea #1: Precompute Everything
One idea is to store for the possible integers , and put them in a hash table mapping from to . Then for each we would check if is in the hash table, where and .
This would require around 137 GB of space ( B/key * keys), plus around 2x overhead for the hash table. This is a possibility – and perhaps leveldb is an option to accomplish this. However, since elliptic curve operations are so slow, the precomputation could take days or longer!
Idea #2: Giant Steps
We can apply the giant steps, baby steps algorithm to the problem. Typically we would precompute values and evaluate values at runtime, but we are going to tune these parameters to decrease runtime work at the cost of memory.
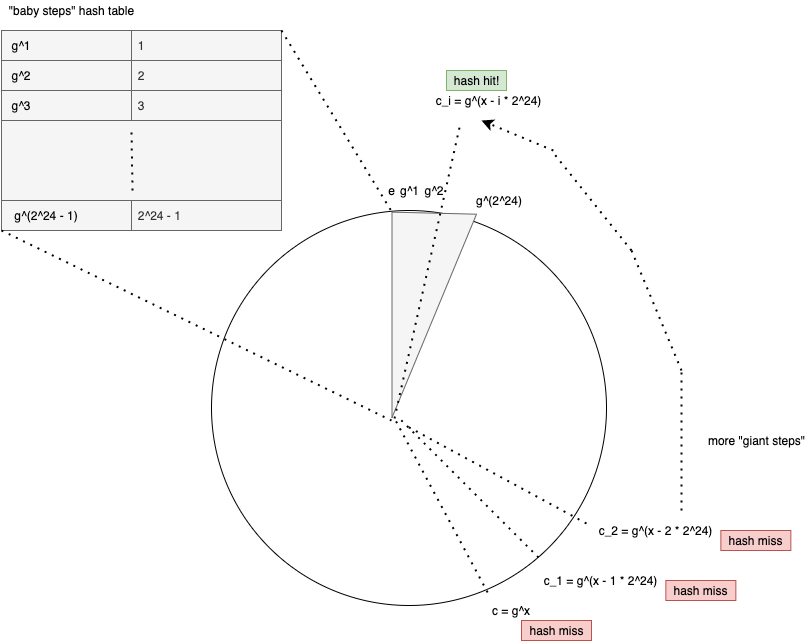
We can trim the work down to precomputed values of and runtime-computed values of . The fewer values we precompute, the more runtime computation is required – we’ll need to tune the parameters.
On my laptop, doing precomputations took about 10 minutes, but I recovered the secret in only seconds – pretty close. Any more precomputation (i.e., ) ran into RAM issues. This makes sense, since EC keys are ~0.25 KiB, so this would be like a 1GB in-memory hash table in Python…probably a bad idea.
Idea #3: Distribute the Work
I had access to the UF CISE computer lab, so instead of optimizing further, I just spun up 5 web servers and distributed the 250 public keys among them. This computation took 87 seconds – which left 13 seconds to manually copy and paste the keys and resulting hash between the netcat session and the running program.
I did this and got the flag
CTF-BR{Blockchainbandit-is-a-n1c3-w4y-to-become-r1ch}
This is a reference to the “Blockchain Bandit” described here.
Implementation
First, the workers are initialized. Each one constructs the -size hash table. Once that’s done, the orchestrator is run, which offloads the work and concatenates the responses. Then, it prints out the hash.
Orchestrator
from fastecdsa import keys, curve
from fastecdsa.point import Point
from threading import Thread
import requests
import hashlib
import time
import json
import struct
from pubkeys import pub_keys
time1 = time.time()
# transform keys from [(x1, y1), (x2, y2), ...] into [x1, y1, x2, y2, ...]
# so that they can be converted to JSON
load = []
for a in pub_keys:
load.append(a[0])
load.append(a[1])
def send(url, job, output):
""" Send job request to a node """
res = requests.request(method='get', url=url, json={ 'data': job })
for r in json.loads(res.text):
output.append(r)
output = [[], [], [], [], []]
jobs = [load[:100], load[100:200], load[200:300], load[300:400], load[400:]]
urls = [
'http://lin114-11.cise.ufl.edu:5000/',
'http://lin114-10.cise.ufl.edu:5000/',
'http://lin114-09.cise.ufl.edu:5000/',
'http://lin114-08.cise.ufl.edu:5000/',
'http://lin114-07.cise.ufl.edu:5000/',
]
# create threads
threads = []
for out, job, url in zip(output, jobs, urls):
threads.append(Thread(target=send, args=(url, job, out)))
# run work
for t in threads: t.start()
for t in threads: t.join()
# combine output
secret_ints = []
for out in output:
for p in out:
secret_ints.append(p)
# convert to bytes
secret = struct.pack(">I", secret_ints[0])
for s in secret_ints[1:]:
secret += struct.pack(">I", s)
# print correct hash
print(hashlib.sha256(secret).hexdigest())
# how long? (around 87 seconds)
print(time.time() - time1)Worker
from fastecdsa import keys, curve
from fastecdsa.point import Point
import random
from collections import defaultdict
from flask import Flask, jsonify, request
bits = 32
giantstep = 24
babysteps_to_i = defaultdict(int)
# pre-compute baby steps
G = keys.get_public_key(1, curve.P256)
babysteps_to_i[G.x] = 1
curr = G
for i in range(2, 1 << giantstep):
if i % 1000 == 0: print(i)
curr = curr + G
# discard the y-component and we're still fine (with overwhelming probability)
babysteps_to_i[curr.x] = i
# pre-compute giant steps
giantsteps = [keys.get_public_key(0, curve.P256)]
G = keys.get_public_key(1 << giantstep, curve.P256)
curr = G
giantsteps.append(G)
for i in range(2, 1<<(bits - giantstep)):
if i % 1000 == 0: print(i)
curr = curr + G
giantsteps.append(curr)
# order of finite field in P-256 curve
order = 115792089210356248762697446949407573529996955224135760342422259061068512044369
def solve(pubkeys, result):
""" finds secret for each key in `pubkeys` using precomputed values """
for p in pubkeys:
# parse key
x = int(p[0], 16)
y = int(p[1], 16)
point = Point(x, y, curve=curve.P256)
isDone = False
# for each possible concatenation
for r_i in range(1, 2**8):
if isDone: break
# generate concatenation k
k = 0
for i in range(8): k = (k << 32) + ((r_i >> i) % 2)
# candidate for pG
kinv = pow(k, (order - 2), order)
pG = kinv * point
# check if pG has p < 2^32 using giant steps, baby steps
for i in range(0, 1 << (bits - giantstep)):
babypoint = pG - giantsteps[i]
# use hash table to check 2^24 baby-points
keyi = babysteps_to_i[babypoint.x]
if keyi != 0:
result.append(keyi + (i<<giantstep))
isDone = True
break
# web server
app = Flask(__name__)
@app.route('/')
def get():
d = request.get_json()['data']
pubkeys = []
for i in range(0, len(d), 2):
pubkeys.append((d[i], d[i+1]))
out = []
solve(pubkeys, out)
return jsonify(out)
if __name__ == '__main__':
app.run(host='0.0.0.0')