Building a fast spline renderer with HTML5

I made a spline-drawing program with HTML5 Canvas. This write-up describes some of the methods I used.

You can check out the demo here, and you can find the source code here.

Background

Given points $(t_0, x_0), (t_1, x_1), ..., (t_n, x_n)$, a cubic spline is a piecewise cubic polynomial $f(t)$ that passes through each $(t_i, x_i)$ pair, and has the property that $f$, $f'$, and $f''$ are continuous on $[t_0, t_n]$.

For any set of points, there are many different cubic splines that interpolate them.

Cubic splines have $4n$ coefficients, but there are only $4n - 2$ constraints on their coefficients. We will impose two more constraints, and then we can uniquely define a “natural” cubic spline from the control points.

A natural cubic spline is a cubic spline that also satisfies the condition that $f''(t_0) = f''(t_n) = 0$.

Representing Parametric Splines

Given a set of points $r_0 = (x_0, y_0), r_1 = (x_1, y_1), ... , r_n = (x_n, y_n)$, we want to construct a spline that interpolates them in order.

We can’t do this with splines in a single dimension. So we parameterize, and consider a parametric function $f(t) = (x(t), y(t))$ that interpolates $(t_0, r_0), (t_1, r_1), ... , (t_n, r_n)$. You can show that if $x(t)$ and $y(t)$ are splines for $\{(t_i, x_i)\}$ and $\{(t_i, y_i)\}$, then $f(t)$ will be a spline for $\{(t_i, r_i)\}$.

There are basically no restrictions on our choice of $t_i$ (except that $t_i < t_{i+1}$). And our choice of $t_i$ dramatically affects the parametric natural spline we get.

We have a couple of nice options for our $t_i$.

• We can choose $t_0 = 0, t_1 = 1, ... , t_n = n$. The result will be the only “smooth” ($f'$ and $f''$ continuous) cubic piecewise polynomial that travels through the $r_i$ at one-second intervals. Also, this choice of evenly spaced $t_i$ simplifies some of the spline calculations.

• Or, we can choose our $t_i$ to be proportional to the Euclidean distance between $r_i$ and $r_{i+1}$. The result will be a spline with relatively constant speed. Visually, the generated spline is a very smooth-looking interpolation of $r_0, r_1, ..., r_n$.

I implemented both of these – you can use the “MODE” toggle to switch between choices 1 and 2 (2 is the default).

Finding the closest spline segment to a point

Given a point $(x, y)$ and a parametric cubic spline $f(t) = (x(t), y(t))$, we want to find the segment of the spline $(x, y)$ is closest to.

Since splines are continuous, we can just apply basic optimization techniques:

1. For each spline segment $f_i$, find the critical points of the distance $D_i(t)$.
2. The critical point $s$ with the smallest $D_i(s)$ is the absolute minimum for this spline.
3. Choose the spline segment with the smallest minimum distance.

But we run into a problem: the squared distance from a cubic function to a point is a sixth-degree polynomial, so the derivative is a fifth-degree polynomial. There is no explicit formula!

Durand-Kerner

We used a simple iterative algorithm, called Durand-Kerner, to find all five roots simultaneously. Notice that some of the roots will be complex numbers – we will discard these.

The Wikipedia article is a pretty good read, but the basic idea of Durand-Kerner is the fact that if

$$P(x) = (x - r_1)(x - r_2)(x - r_3)(x - r_4)(x - r_5)$$

then we can derive that

$$r_1 = x + \frac {P(x)} {(x - r_2)(x - r_3)(x - r_4)(x - r_5)}$$

and notice that a fixed point iteration on the second expression (and its related $r_2, r_3, ...$ versions) can solve for all five roots simultaneously. We choose initial complex values $a_0, b_0,..., e_0 \in C$. Then we compute

$$a_{i + 1} = a_i + \frac {P(a_i)} {(a_i - b_i)(a_i - c_i)(a_i - d_i)(a_i - e_i)}$$ $$b_{i + 1} = b_i + \frac {P(b_i)} {(b_i - a_i)(b_i - c_i)(b_i - d_i)(b_i - e_i)}$$ $$...$$ $$e_{i + 1} = e_i + \frac {P(e_i)} {(e_i - a_i)(e_i - b_i)(e_i - c_i)(e_i - d_i)}$$

until $\|a_{i+1} - a_i\| < \epsilon$, $\|b_{i+1} - b_i\| < \epsilon$, $...$, and $\|e_{i+1} - e_i\| < \epsilon$ for some tolerance $\epsilon$.

Pseudocode

function distToCurve(curve: Curve, { x, y }: Point) {
    // always check endpoints
    const tValuesToCheck = [0.0, 1.0];

    // find other local extrema of distance function
    const coeffs = getCoefficientsOfSquaredDistance(curve, { x, y });
    const roots = durandKernerRoots(derivative(coeffs));
    
    for (const t of roots) {
        // only consider t-values within the segment
        if (t >= 0.0 && t <= 1.0) {
            tValuesToCheck.push(t);
        }
    }

    // check each point and return minimum distance
    return Math.min(...tValuesToCheck.map(t => dist(curve.at(t), { x, y }));
}

Other methods

I read an interesting paper about using Newton’s method and quadratic minimization to solve this problem. The authors were using cubic splines to model roads for a driving simulator, and, in real-time, wanted to find where the vehicle was on the road given the $(x, y, z)$ coordinates.

Drawing the curve

The last problem is to render the cubic polynomial continuously (without gaps) on a grid of pixels.

The problem is in how we choose which t-values to draw. If we pick 100 evenly-spaced t’s, then our curve might look like this:

Even if we pick 1000 evenly-spaced t’s, our rendered curve will still have small local defects where the velocity is high.

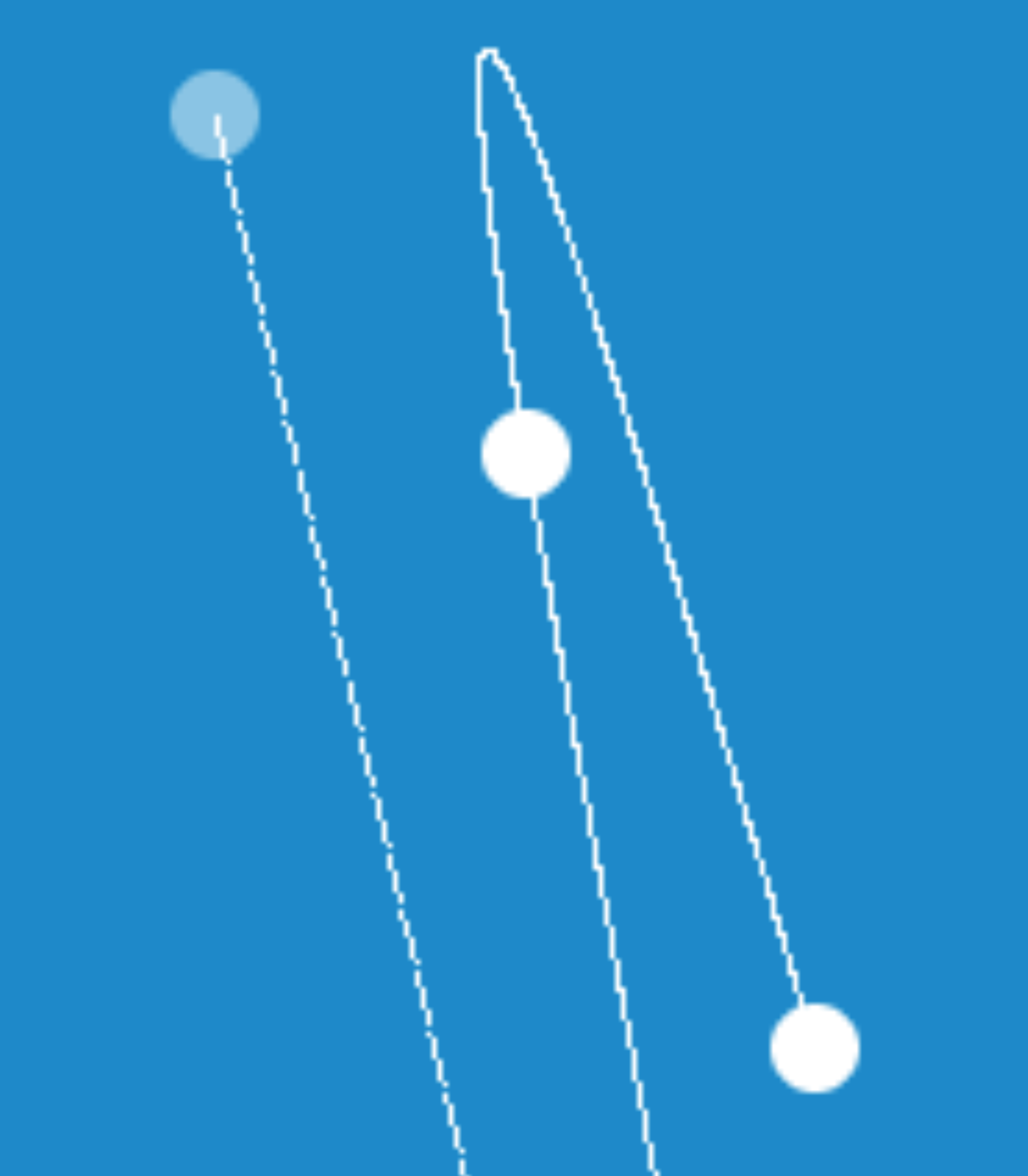
The problem with using a bigger number of evenly-spaced t-values is that it’s a lot of wasted work to draw the points (since when the curve has low velocity, the image of the t-values will overlap). But, if we’re adaptive in how we choose the t-values, we can produce an image that looks like

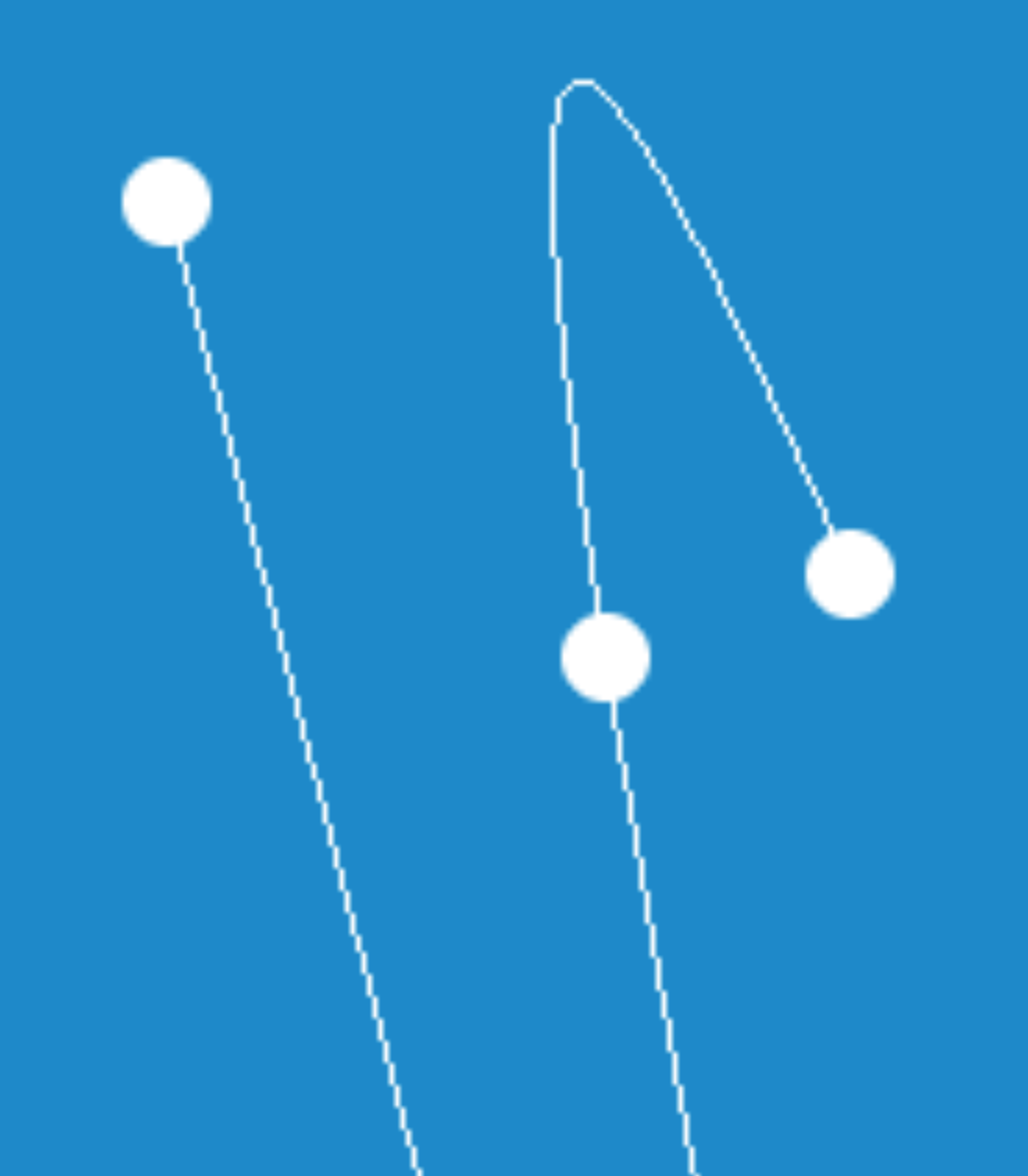
without doing thousands of unnecessary computations. In other words, we want to find a minimal set of $t_i$, where $0 = t_1 < t_2 < ... < t_{k-1} < t_k = 1$, such that, if we plot the points $f(t_1), f(t_2), ..., f(t_k)$ as the 1x1 pixels they live inside, then those pixels will be adjacent.

We will derive an adaptive algorithm to find the $t_i$. Let’s impose an additional restriction – if we have for all $1 \le t \le k$ that

$$\max(|x(t_{i+1}) - x(t_i)|, |y(t_{i+1}) - y(t_i)|) = 1$$

then our set of squares will certainly be adjacent. Let’s consider just the $x$-dimension. We want to find a $t_{i+1}$ such that

$$|x(t_{i+1}) - x(t_i)| = 1$$

If we approximate $x(t_{i+1})$ from $x(t_i)$ using

$$x(t_{i+1}) \approx x(t_i) + x'(t_i) (t_{i+1} - t_i)$$

then we have that

$$|x'(t_i) (t_{i+1} - t_i)| \approx |x(t_{i+1}) - x(t_i)| = 1$$

and

$$t_{i+1} \approx t_1 + \frac {1}{|x'(t_i)|}$$

and by the same argument for $y(t)$, we have that the optimal $t_{i+1}$ can be approximated with

$$t_{i+1} \approx t_1 + \min(\frac {1}{|x'(t_i)|}, \frac{1}{|y'(t_i)|})$$

If the first-derivative approximation for $x(t_{i+1})$ is close (which it “usually” is), the $t_i$ generated will give us connected squares. Even better, the number of $t_i$ generated will be close to the minimal number of $t_i$ that still give us connected squares (since our $t_i$ were chosen so that $\max(\Delta x, \Delta y)$ = 1)

Here is the pseudocode for the adaptive step-size.

let dt = 0;
for (let t = 0; t < 1; t += dt) {
    // evaulate x(t), y(t), x'(t), y'(t)...
    
    // update t using adaptive algorithm
    dt = Math.min(1 / Math.abs(dx), 1 / Math.abs(dy));

    // plot the point
    putPixel(x, y, color);
}

Conclusion

I had a lot of fun building this, and I got to learn about a simultaneous root-finding algorithm and I got to figure out a decent way to do adaptive polynomial graphing.

Thanks for reading!